



Next: Using pplane2d.m
Up: Required Files and Descriptions
Previous: ccquad.m
Contents
This represents the system associated with the 2nd
order, nonlinear, homogeneous ODE with constant coefficients that
describes the motion of a damped pendulum.
The linearization of this system is accomplished via the four
partial derivatives
evaluated at any critical point
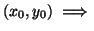
Once the linearization has been formed, we use cclin.m with
to investigate stability about each 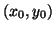 .
.
The symbolicplot option `eigenvals' is useful only for
the linearization.
Michael Renardy
2000-05-12
![\begin{eqnarray*}
\begin{array}{rcrcr} x' &=& y &=& F(x,y) \\ y' &=&
-\omega^2\...
... \right]\,
\left[\begin{array}{c}\sin x \\ y\end{array}\right]
\end{eqnarray*}](img111.gif)
![\begin{eqnarray*}
\begin{array}{rcrcr} x' &=& y &=& F(x,y) \\ y' &=&
-\omega^2\...
... \right]\,
\left[\begin{array}{c}\sin x \\ y\end{array}\right]
\end{eqnarray*}](img111.gif)
![\begin{displaymath}\; \Longrightarrow \;\; \mbox{\tt A = [$\;$];} \quad \mbox{\tt B = [$0$, $1$;
$-\omega^2$, $-\gamma$];}\end{displaymath}](img112.gif)
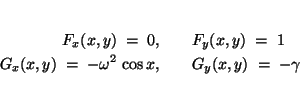
![\begin{eqnarray*}
\left[\begin{array}{c}x' \\ y'\end{array}\right] &\approx& \le...
...{array}{c}x \\ y\end{array}\right] \quad\mbox{near $(x_0,y_0)$}
\end{eqnarray*}](img114.gif)
![\begin{displaymath}\mbox{\tt A = [0,1; $-\omega^2\,\cos x_0$,$-\gamma$];} \quad
\mbox{\tt B = [$\;$];}\end{displaymath}](img115.gif)