Example

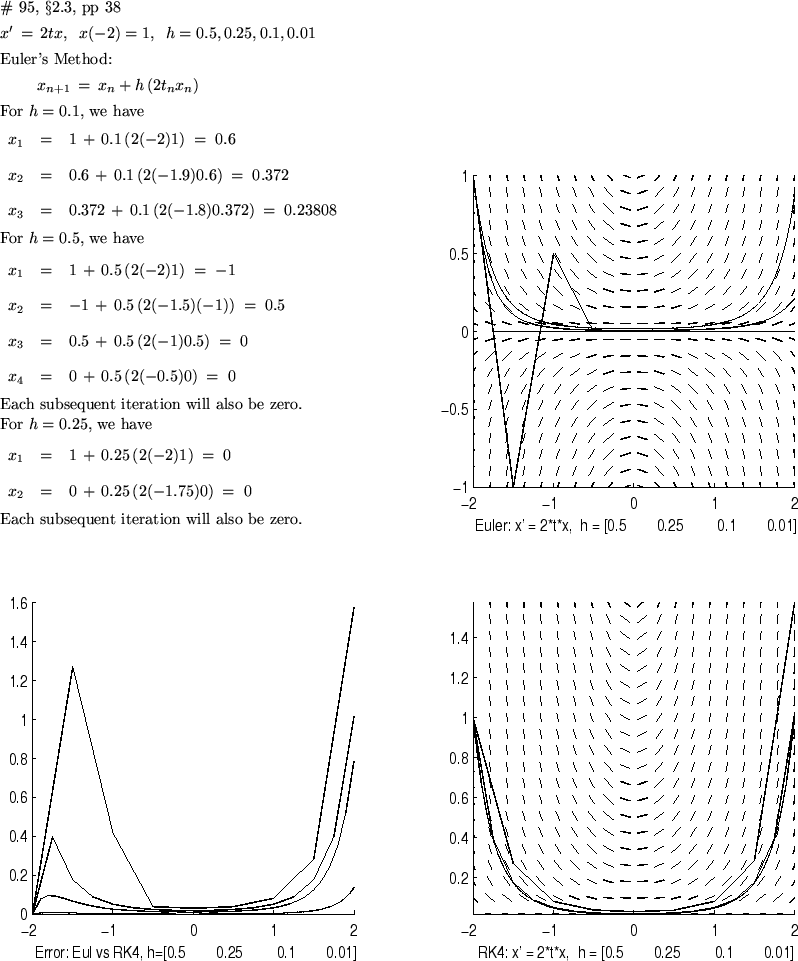
Use Euler's method to approximate a solution to the ODE $x'= 2tx$. By hand, set up the iterating equation and solve for three iterations using the initial condition $x(-2) = 1$ and step size $h = 0.1$. Next investigate both Euler's method and the 4th order Runge-Kutta method graphically using num3plot with the four step sizes $h = 0.5,\; 0.25,\; 0.1,\;, 0.01$. Identify each plot with its respective step size. Explain the rather odd behavior for $t > 0$ with $h = 0.5, \; 0.25$ when all plots are compared. You may need to calculate a few Euler iterations by hand for these step sizes. (Does this suggest more than one way that step size can affect results?)

1. Iterating equation $x_{n+1} \,=\, x_n + h \,(2t_n x_n)$ with $h = 0.1, \; t_0 = -2, \; x_0 = 1 \; \Longrightarrow \;$
   $$\begin{eqnarray*} x_1 &=& 1 \,+\, 0.1 \,(2(-2)1) \;=\; 0.6 \\ [1ex] x_2 &=& 0.6 ... ...\ [1ex] x_3 &=& 0.372 \,+\, 0.1 \,(2(-1.8)0.372) \;=\; 0.23808 \end{eqnarray*}$$
   
   
   
   
   

2. Change only the following in initn.m

    
   ftx='2*t*x'; 
   eulerfcn='x+h*(2*t*x)'; 
   hvec=[.5,.25,.1,.01]; 
   t0=-2; tf=2; x0=1;
   

   Save, then type initn to initialize the variables (or copy-and-paste at the Emporium).
3. Type num3plot
4. Here one should investigate and show results such as in Item 4, pp , for eulplot.
   
   For $h = 0.5$, we have
   $$\begin{eqnarray*} x_1 &=& 1 \,+\, 0.5 \,(2(-2)1) \;=\; -1 \\ [1ex] x_2 &=& -1 \,... ...0.5) \;=\; 0 \\ [1ex] x_4 &=& 0 \,+\, 0.5 \,(2(-0.5)0) \;=\; 0 \end{eqnarray*}$$
   
   
   
   
   
   Each subsequent iteration will also be zero.
   For $h = 0.25$, we have
   $$\begin{eqnarray*} x_1 &=& 1 \,+\, 0.25 \,(2(-2)1) \;=\; 0 \\ [1ex] x_2 &=& 0 \,+\, 0.25 \,(2(-1.75)0) \;=\; 0 \end{eqnarray*}$$
   
   
   
   
   
   Each subsequent iteration will also be zero.
5. The finished product is on the next page. (Note: your work in the upper left will be neatly hand written, not typed.) Also be sure to identify which approximation goes with which stepsize from hvec for all three graphs.