Using num3plot.m

1. Set up the appropriate iterating equation for Euler's method that pertains to the ODE being considered. If instructed, solve a few iterations of the method by hand.
2. Make the necessary entries in initn.m.

   ftx = '$f(t,x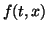)$'; (RHS of $x' \,=\, f(t,x)$)
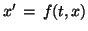   eulerfcn = ' 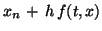$x_n \,+\, h\,f(t,x)$'; (Iterating equation for Euler's method)
   hvec = [ 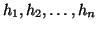$h_1, h_2, \dots, h_n$]; (Desired step sizes)
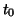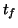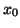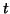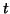   t0 = $t_0$; tf = $t_f$; x0 = $x_0$; (initial $t$-value, final $t$-value, initial 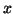$x$-value, respectively)

   Save and type initn (or copy-and-paste at the Emporium).
3. Type num3plot This may take up to a few minutes depending on your machine, the choice of step size(s), and/or the difficulty of the ODE. In your Figure window, you should have three plots.
   1. Upper right contains Figure 1, the Euler approximations for each of the step sizes in hvec, plotted on top of the slope field.
   2. Lower right contains Figure 3, the RK4 approximations for each of the step sizes in hvec, plotted on top of the slope field.
   3. Lower left contains Figure 2, a graphical representation of errors between the Euler solutions and Runge-Kutta solutions for each step size in hvec. t is the independent variable, and error is plotted as the dependent variable.
4. Make a visual check that your hand computations match the appropriate plot(s) in Figure 1. Check that the solutions for each method tend to follow the slope field as the step size gets smaller. If all appears correct, print a copy of the display.
5. In the upper left of your printout, neatly and orderly rewrite the work you did for Euler's method in Item 1.