



Next: First Order ODEs Numerically
Up: Using hw3plot.m
Previous: Using hw3plot.m
Contents
Use hw3plot.m to create a slopefield, numerical plot, and
plot of the symbolic solution to the ODE
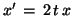 .
.
- Separable equation
- ftx = `2*t*x';
initax = [1,4,-2,0];
t0 = 0;
x0 = 0; C = 1;
ftxsln = `C*exp(t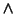 2)';
2)';
- slopef(ftx,N) results in
![\begin{picture}(5,5.5)
\put(1,0){\includegraphics [width=5cm,height=5cm]{inst2f01.ps}}
\end{picture}](img41.gif)
Change initax = [-2,2,-2,2]; then slopef(ftx,N) results in
![\begin{picture}(5,5.5)
\put(1,0){\includegraphics [width=5cm,height=5cm]{inst2f02.ps}}
\end{picture}](img46.gif)
- Running sol1 and placing pointer at about (1,1)
results in
![\begin{picture}(5,5.5)
\put(1,0){\includegraphics [width=5cm,height=5cm]{inst2f03.ps}}
\end{picture}](img51.gif)
- From the display we have t0 = 1.0932 and x0 = 0.95208
which we enter into init.m.
- Using
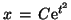 , we solve
, we solve
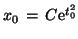 ; i.e.,
; i.e.,
which we enter into init.m.
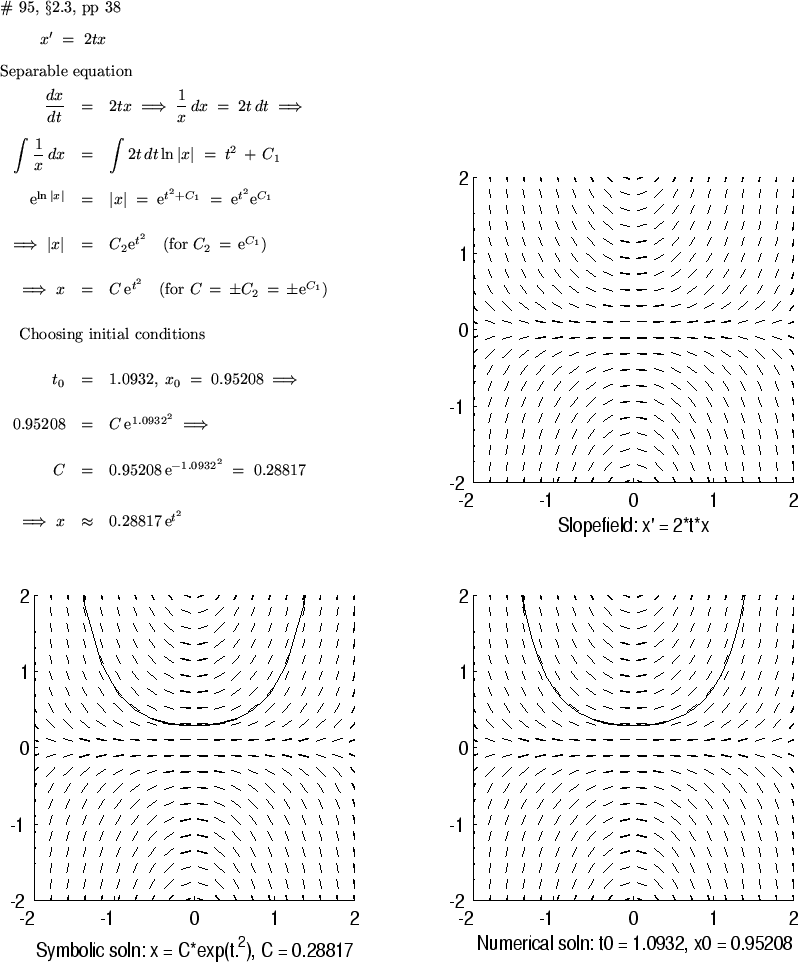
Completing Items 7-10, we obtain the finished product illustrated on
the next page. (Note: your work in the upper left will be neatly hand
written, not typed.)
Michael Renardy
2000-05-12
.
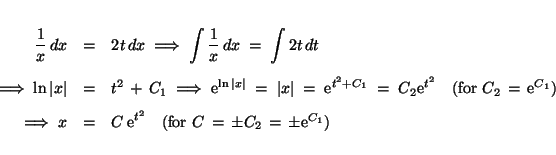
![\begin{picture}(5,5.5)
\put(1,0){\includegraphics [width=5cm,height=5cm]{inst2f01.ps}}
\end{picture}](img41.gif)
![\begin{picture}(5,5.5)
\put(1,0){\includegraphics [width=5cm,height=5cm]{inst2f02.ps}}
\end{picture}](img46.gif)
![\begin{picture}(5,5.5)
\put(1,0){\includegraphics [width=5cm,height=5cm]{inst2f03.ps}}
\end{picture}](img51.gif)
![\begin{eqnarray*}
t_0 &=& 1.0932, \; x_0 \;=\; 0.95208 \; \Longrightarrow \;0.95...
... \;\\ [1ex] C &=& 0.95208 \,\mbox{e}^{-1.0932^2}
\;=\; 0.28817
\end{eqnarray*}](img61.gif)
