



Next: Example
Up: First Order ODEs Symbolically
Previous: Example 2
Contents
Tying graphical, symbolic, and numerical representations together
is an important goal of this course. hw3plot.m is designed
to bring these together on one page.
- Solve the indicated ODE by hand using whichever method is
appropriate to the textbook section containing the problem. This is to
be done on scratch paper.
- Make the appropriate entries in init.m for ftx and
ftxsln. Make an educated guess for initax-values. Be sure
some value is entered for each of t0, x0, C. Save then type
init in the command window to initialize the variables (or
copy-and-paste in the Emporium).
- Type slopef(ftx,N) to check that the plot window size
is appropriate. Adjust initax in init.m if
necessary. Save then type init in the command window (or
copy-and-paste in the Emporium).
- Type sol1 and choose initial conditions (i.e.,
(t0,x0)) that produce a solution illustrating the ``interesting''
behaviour of the ODE. You may need to experiment here.
- Note the t0 and x0-values returned by sol1 at
the bottom of the plot and enter these values in init.m.
- Solve for C by substituting t0 and x0 into the
general symbolic ODE solution you obtained by hand, then enter the
result into init.m.
- Save init.m then type init in the command window
to initialize the new variables (or copy-and-paste in the Emporium).
- Type hw3plot. A ``y'' answer to ``Do you already have a
separate figure window for hw3plot? (y/n)'' creates a new MATLAB
Figure window specifically for hw3plot. If you have already
used hw3plot in this session, an appropriate window should
already exist, and you can answer ``n ``.
In your Figure window,
you should have three plots.
- Upper right contains Figure 1, the slopefield for ftx.
- Lower left contains Figure 2, your symbolic solution for the
C obtained with the initial conditions (t0,x0). This is
plotted over the slope field.
- Lower right contains Figure 3, the numerical solution of
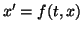 determined via sol1 plotted over the slope field.
determined via sol1 plotted over the slope field.
- If the solutions to Figures 2 and 3 do not match, there are
generally two possibilities: (a) the existence and uniqueness
theorems governing ODEs have been violated; or (b) you did not solve
the ODE properly or made an error solving for C. In both cases,
the numerical solution from MATLAB is usually correct. In case (a),
your symbolic plot should look like the numerical plot except that
yours will contain more of the graph. Your graph has ``jumped'' over
a discontinuity. There is nothing to change at this time, but you
should include an explanation to this effect. If your graph looks
differnt in other ways, you are probably in case (b). Check your
work and any of Items 1-8 that are appropriate for errors.
If the solutions to Figures 2 and 3 are the same, print a copy of
the display.
- In the upper left of your printout, neatly and orderly rewrite
the work you did to solve the ODE in Item 1 and to find C.
Subsections




Next: Example
Up: First Order ODEs Symbolically
Previous: Example 2
Contents
Michael Renardy
2000-05-12
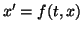 determined via sol1 plotted over the slope field.
determined via sol1 plotted over the slope field.