



Next: Example 2
Up: Examples
Previous: Examples
Contents
When you first copy init.m, it should be
set to run this example.
Plot a slopefield for
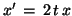 over a rectangle
illustrating the general characterisics of the ODE. Then plot
one solution to the ODE within this rectangle.
over a rectangle
illustrating the general characterisics of the ODE. Then plot
one solution to the ODE within this rectangle.
- Change only the following in init.m
ftx = '2*t*x'; (``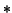 '' indicates multiplication)
'' indicates multiplication)
initax = [1,4,-2,0];
Save then type init in the command window to initialize the
variables (or copy-and-paste in the Emporium).
- See the example for slopef, page
![[*]](/people/linnell/Icons/cross_ref_motif.gif) ,
to investigate the window size initax = [1,4,-2,0]; then
make the change to initax = [-2,2,-2,2]; in init.m.
Save then type init in the command window to initialize the
variables (or copy-and-paste in the Emporium).
,
to investigate the window size initax = [1,4,-2,0]; then
make the change to initax = [-2,2,-2,2]; in init.m.
Save then type init in the command window to initialize the
variables (or copy-and-paste in the Emporium).
- Type sol1. Answer ``y'' to draw new slopefield
![\begin{picture}(5,5.5)
\put(1,0){\includegraphics [width=5cm,height=5cm]{inst2f02.ps}}
\end{picture}](img46.gif)
- Have MATLAB draw a solution close to
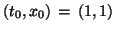 by clicking near that initial condition on the slopefield.
by clicking near that initial condition on the slopefield.
![\begin{picture}(5,5.5)
\put(1,0){\includegraphics [width=5cm,height=5cm]{inst2f03.ps}}
\end{picture}](img51.gif)
From the graphics display we observe the actual
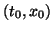 -value. (In this case
-value. (In this case
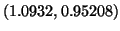 .)
.)




Next: Example 2
Up: Examples
Previous: Examples
Contents
Michael Renardy
2000-05-12
over a rectangle illustrating the general characterisics of the ODE. Then plot one solution to the ODE within this rectangle.
'' indicates multiplication)
![\begin{picture}(5,5.5)
\put(1,0){\includegraphics [width=5cm,height=5cm]{inst2f02.ps}}
\end{picture}](img46.gif)
![\begin{picture}(5,5.5)
\put(1,0){\includegraphics [width=5cm,height=5cm]{inst2f03.ps}}
\end{picture}](img51.gif)