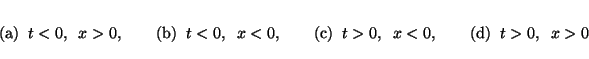Next: Using sol1.m
Up: Using slopef.m
Previous: Using slopef.m
Contents
When you first copy init.m, it should be
set to run this example.
Plot the slopefield for
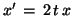 over the rectangle
over the rectangle
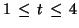 ,
,
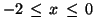 . Investigate
whether this rectangle gives a good overall picture of the ODE
behavior. If not, plot over a better rectangle.
. Investigate
whether this rectangle gives a good overall picture of the ODE
behavior. If not, plot over a better rectangle.
- Change only the following in init.m
ftx = '2*t*x'; (``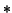 '' indicates multiplication)
'' indicates multiplication)
initax = [1,4,-2,0];
Save then type init in the command window to initialize the
variables (or copy-and-paste in the Emporium).
- Type slopef(ftx,N) to obtain
![\begin{picture}(5,5.5)
\put(1,0){\includegraphics [width=5cm,height=5cm]{inst2f01.ps}}
\end{picture}](img41.gif)
Since
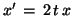 represents the slope, we should also
consider when
represents the slope, we should also
consider when 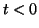 and
and 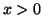 . Suppose we try the symmetric
rectangle
. Suppose we try the symmetric
rectangle
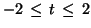 ,
,
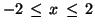 .
.
- This time change only
initax = [-2,2,-2,2];
Save then type init in the command window (or copy-and-paste
in the Emporium).
- Type slopef(ftx,N) to obtain
![\begin{picture}(5,5.5)
\put(1,0){\includegraphics [width=5cm,height=5cm]{inst2f02.ps}}
\end{picture}](img46.gif)
Build your intuition: Does this picture match the general slope
behavior indicated by
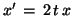 ? Look at the following
cases
? Look at the following
cases




Next: Using sol1.m
Up: Using slopef.m
Previous: Using slopef.m
Contents
Michael Renardy
2000-05-12
over the rectangle
,
. Investigate whether this rectangle gives a good overall picture of the ODE behavior. If not, plot over a better rectangle.
'' indicates multiplication)
![\begin{picture}(5,5.5)
\put(1,0){\includegraphics [width=5cm,height=5cm]{inst2f01.ps}}
\end{picture}](img41.gif)
![\begin{picture}(5,5.5)
\put(1,0){\includegraphics [width=5cm,height=5cm]{inst2f02.ps}}
\end{picture}](img46.gif)